The Game:

Nemo's Secret The Nautilus is a hidden object game. The primary goal of the game is to find the Nautilus.

You start at Nemo's house. Find a way in then, find a map indicating where the Nautilus may be found.

Head to the docks and fix a boat. Sail to the location marked on the map. Dive below and find the Nautilus. It's just out of reach so you must find a way to get to it.

Once at the Nautilus you will need to make repairs and solve many puzzels designed to stop you. At one point you will come across the need for a key which you must make. But to make the key you need to solve the clam shell board puzzel.

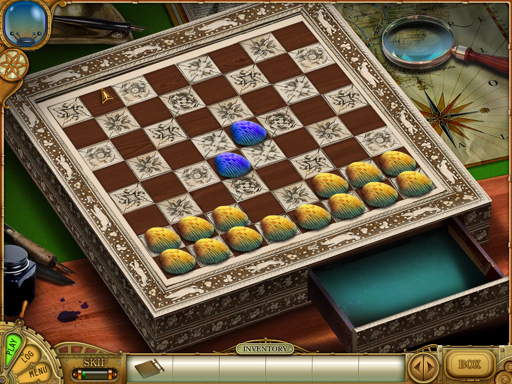
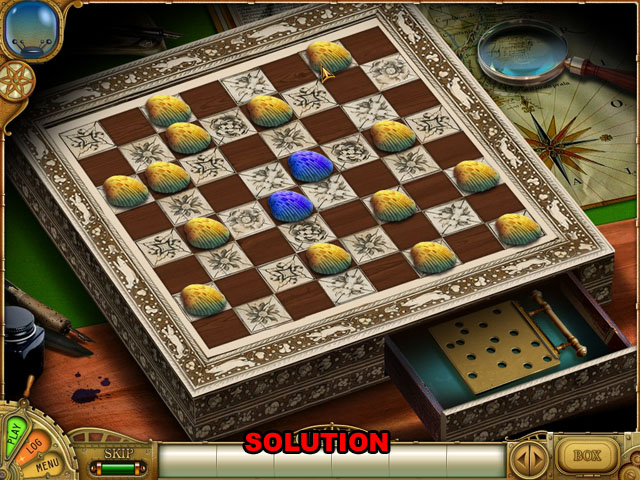
The above picture is the boards initial layout.

You insert the copper plate (which needs to be found), position the yellow clam shells (the blue ones are fixed and aren't moveable) in the correct position which will cause the copper plate to be stamped with the proper holes.

Note:

The timings seen below varies slightly from run to run. The timings shown in the images came from that program. The timing in the tables came from the Total Solutions calculator. A single line of code was added to stop the calculations. This produces a small reduction in calculation time compared to the normal code in the calculators.

Before you start solving the puzzel the ticker tape devices (hints from Nemo) gives you a clue as to what you need to do. As you may note it says 2 shells in each row, 2 shells in each column and 2 shells on a diagonal.

If you look in your log you will note only the column requirement is mentioned. There is another clue given elsewhere that mentions both the row and column requirements.

After trying a lot of combinations over several hours on several days it became obvious to me it would take a computer to figure out the solution.

The board consist of 8 rows by 8 columns for a total of 64 squares. There are 14 yellow shells and 2 blue shells for a total of 16 shells. This leave 48 empty squares.

I designated the row furthest from the viewer as row 0 (top row) and closest row to the viewer as row 7 (bottom row). The columns are number 0 on the far left to 7 on the far right. There are 2 main diagonals, top-left to bottom-right and top-right to bottom left, plus a lot of minor diagonals, starting at row 0 column 1 down and to the right. Then starting at row 0 column 6 down to the left. Then row 1 column 0 down and to the right. Finally starting at row 1 column 7 down and to the left.

Since there is no difference between the yellow clam shells a lot of redundant combinations can be skipped. Also all 16 clam shells are required for the solution so all combinations that use less can be skipped.

From the initial positions the first move would be to move shell at 6,0 (row,col) to 0,0. This is board combination 1 (0 is the initial board layout). A check routine is called and the display is updated. If this results in a solution, then the program stops. Otherwise, shell at 6,1 is moved to 0,1 and checked. The shell at 0,1 is stepped to each following empty square which is 48 steps. At the end of this the board number should be 49. Board 0 (initial), first move to 0,1 and then 48 empty squares. The shell should have ended up at 6,4 and is moved back to it starting position at 6,1. Now the process is repeated with the shell at 6,2. The board number at the end of this should be 96 with the shell ending at position 6,4. This process is repeated so that all 13 shells have been moved to 0,1 and stepped thru all 48 empty slots. This number of total boards would be 4913 or 9,387,480,337,647,754,305,649. This would only be the first combinations. The next step would be to move 6,0 and 6,1 to 0,0 and 0,1 and start by moving the others one at a time thru the 48 empty squares. Then you would repeat this with 3 shells at the top and move the other 11 thru and so on and so on. This many boards will take decades if not centuries to calculate.

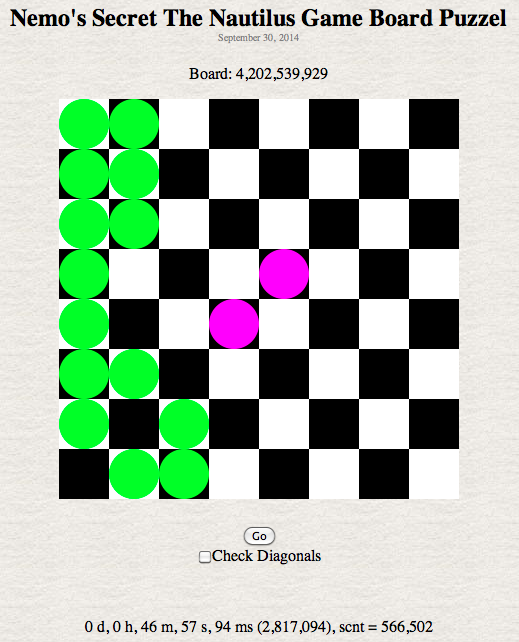
So we apply a little logic. To reduce the combinations we must limit the number of moves a shell needs to make. The solution was to enforce 2 rules: only 2 shells in a row and only 2 shells on a mayor diagonal. There are 2 blue shells already on a major diagonal that can't be moved, so any squares on that diagonal are considered not empty for the move routine. Now that there are a fixed pair of shells on a row, that reduces the empty squares for a single shell to move onto down from 48 to 5. So Each row has 21 positions ( 20 moves plus the initial row starting position ) except rows 3 and 4 which only have 1 moveable shell. The total number of positions on one of these rows is 7 ( 6 moves plus the initial row starting position ). Total number of boards is 216 * 7 * 7 + 1 ( board 0 ) or 4,202,539,930.

The first time the program ran it took around 28 hrs to complete. Since javascript is single threaded the display is only updated when the program ends so all the code to update the display after every move was just wasting time. Also all the embedded loops were not very efficient.

The first speed up of code was to updated the display only after all the calculations are done.

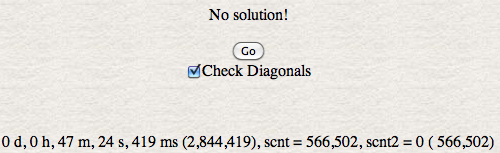
The program came up with no solution to the problem. This indicated to me that the minor diagonals where probably not apart of the solution, so they were placed in their own function but never called.

The giant grid array (the board) was replaced with a simple array that tracked the 14 yellow clam shells mathematically. The move routine was reduced to 2 functions, 1 to move the double shells on a row and 1 to move the single shell on a row. If a row was at the end when it was called to make a move it reset the shells to their starting position on it's row and set a flag which caused the function to be called again with the next row. If this flag was set by the last row then the done flag was set. I then added timers to see how long each row took to execute and how long it took to process all board combinations. The results are below.

Compute Total Solutions:

This calculator computes the total number of board positions checked and the total number of solutions found. The checkBoard function checks the columns and top-left to bottom-right diagonal. If the Check Diagonals check box is checked then a solution found with the checkBoard function calls checkBoard2 function which also checks all the minor diagonals.

Displayed at the bottom is the time it took to run the program. The number in the first set of parentheses is the time in milliseconds. The scnt ( solution count ) value is the total number of solutions found. The scnt2 is the total number of solutions found with the checkBoard2 function. The number in parentheses following scnt2 is the number of times the checkBoard2 function was called. This should equal the scnt value. When you click the Go button the program will make the calculations.

You may have noticed that according to the rules there are 566,502 solutions. Even at 5 secs an entry it would take me around 787 hours (33 days) non-stop to enter all possibilities.

Compute Correct Solution:

From the Wiki someone by chance found the solution. This calculator determines what board combination produces the solution (as well as the solution number).

Compute Fast Solution:

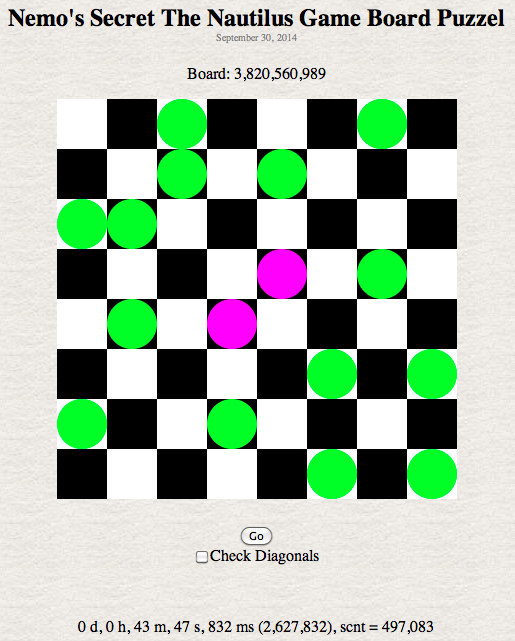
If I reorder the move routines to: 7,5,0,1,3,4,6,4,2 then the time to solution drops as shown below. At 1,498 solutions ( at 5 sec a try ) it would take about 125 hrs ( a little more than 5 days ) to try them all.

Step Function:

This calculator using the step function was used to get the number of steps in a row and the timing of each row. The timing is for the time to make the first step in the given row.

Row	Boards	Mins	Secs	msecs	Raw msec	Solutions		Boards
0	1			0	0	0		1
1	22			0	0	0		211+1
2	422			2	2	0		212+1
3	9,262			12	12	0		213+1
4	64,828			55	55	0		71 * 213+1
5	453,790			258	258	1		72 * 213+1
6	9,529,570		4	910	4,910	951		72 * 214+1
7	200,120,950	1	43	636	103,636	40,122		72 * 215+1
All	4,202,539,930	46	57	94	2,817,094	566,502		72 * 216+1

The Step button will cause a single step to occur in the calculator. The Reset button puts the calculator back to it's starting state. The board below shows the first step and the error found ( column 0 has 7 shells ).

Next Function:

This calculator using the next function allowed me to capture the first 10 solutions and try those. I also captured a few additional solution timings.

Solution	Boards	Mins	Secs	msecs	Raw msec
1	231,525			143	143
2	694,365			379	379
3	712,866			388	388
4	1,203,720			638	638
5	1,333,353			715	715
6	1,463,217			784	784
7	1,463,237			784	784
8	1,574,307			837	837
9	1,574,366			843	843
10	1,602,080			856	856
100	3,834,051		1	978	1,978
1000	11,273,703		5	911	5,911
10,000	53,412,414		27	774	27,774
100,000	726,825,626	6	16	775	376,775
497,083	3,820,560,990	41	55	937	2,515,937

Below is the board position for the first solution found.